“现在,我要在你们面前阐述的时空观产生于实验物理学的土壤,它的力量也源于此。这些观点是根本性的,从此刻起,孤立的空间和孤立的时间注定会消失为影子,只有两者的统一才能保持独立的存在。”
—— 闵可夫斯基 <hr/>上一篇:【篇二十一】 光速不变与洛伦兹变换:“追光”遐想
上回说到:麦克斯韦方程组集中展现了整个十九世纪电磁学探索的伟大成果,但从中推导出的真空中光速c在任何参考系里都是一个常量,这不但与我们的“常识”格格不入,更是让作为物理学根基的经典牛顿时空观摇摇欲坠。在其他物理学家都绞尽脑汁对“以太”模型缝缝补补时,爱因斯坦却创造性地提出了两条基本假设——更普遍的“相对性原理”,以及更严格的“光速不变”。在“光速不变”的前提下构筑出的狭义相对论时空观重塑了人们对宇宙的认知:空间和时间不再彼此孤立,而是被物质运动联系起来,构成了一个密不可分的整体,在不同的参考系中时间和空间坐标可以彼此转换。这样一来,在建立新的时空观之后,我们必然还需要有更加优雅的数学形式将“三维的空间”和“一维的时间”统一在相同的框架下,这便是我们常在科幻小说或电影里听说的概念——四维时空。最初为我们构建四维时空的是德国数学家闵可夫斯基。
——怎样才能将时间和空间统一成四维时空呢?难道仅仅是将空间坐标和时间坐标拼凑起来(例如我们之前广泛使用的\left( x,y,z,t \right) 这样)就可以了吗?显然没有这么简单!这样的“强行拼凑”不但首先连量纲统一都做不到,而且这样得到的“不伦不类”的空间也没有像三维欧几里得空间这样良好的性质,体现不出什么真正的物理内涵。不管怎样,还是得好好设计一番。
“设计”一种新的四维时空,总得依靠一定的理论基础。恰好,之前我们推导洛伦兹变换和相对论时空观下的一些现象时主要只用到了第二条基本假设“光速不变”,现在让我们将视角挪到第一条假设“相对性原理”来——它的表述是“一切惯性系中的物理规律都是相同的”。也就是说,我们接下来的希望是:在洛伦兹变换下,一切物理规律在不同的参考系里都能保持不变,无论是力学规律还是电磁规律。
——这是基于物理学理性与和谐的朴素希望,也是进入“四维”新领域的阶梯。
<hr/>【一】四维时空:闵可夫斯基空间
◆ 相对性原理与“不变量”
要想应用“相对性原理”,第一步需要解决的问题便是:怎么才能说明物理规律在不同的惯性系里保持不变?
早在第一篇中,我们就在伽利略变换的框架里验证了这个问题。当时我们是验证了牛顿第二定律的公式\boldsymbol{F}=m\ddot{\boldsymbol{x}}。假设这原本是\mathrm{S}系中生效的规律(也就是力\boldsymbol{F}、质量m、加速度\ddot{\boldsymbol{x}}都是在\mathrm{S}系中测量出来的结果)。现在换到另一个惯性系\mathrm{S}^{'}系里,通过伽利略变换可以求出在\mathrm{S}^{'}系里测出的“新的”加速度\ddot{\boldsymbol{x}}^{'}=\ddot{\boldsymbol{x}},即方程\boldsymbol{F}=m\ddot{\boldsymbol{x}}^{'}显然也符合牛顿第二定律的形式,这就可以证明牛顿第二定律在伽利略变换下是能在不同惯性系里保持不变的。由此类推,可以证明所有经典力学的规律都能在伽利略变换下保持不变,所以能说经典力学的规律都满足伽利略相对性原理。
——你或许会觉得以上的论证是不完整的,因为\mathrm{S}^{'}系里的牛顿第二定律真正的表达式应当是\boldsymbol{F}^{'}=m^{'}\ddot{\boldsymbol{x}}^{'},你还需要证明在\mathrm{S}^{'}系中测出来的新“力”\boldsymbol{F}^{'}=\boldsymbol{F},以及在\mathrm{S}^{'}系中测出来的新“质量”m^{'}=m才算说明问题。但好在,前者在坐标系平移变换(也是我们所适用的场景下)也是可以证明的,后者在日常生活经验乃至整个经典力学理论框架内似乎是个不容置疑的结论。总而言之:证明不同惯性系下物理规律的不变性,本质上就是证明用时空变换改写后的不同参考系里表述出来的物理规律有着相同的形式。
想证明洛伦兹变换下物理规律能保持不变,也能类似办理。但由于洛伦兹变换中时间和空间相互交叠,还涉及到大量的偏导数,还用这种“代入”、“验证形式是否相同”的“笨办法”就略显笨拙了。而且,这种“办法”只能验证物理规律是否符合相对性原理,如果不符合,需要进行修改,也很难从这种办法直接找到修改的途径。所幸我们找到了另一种途径:探索哪些物理量在洛伦兹变换的前后是保持不变的,也就是在不同参考系里能测出一样的结果。如果能找到这样的“不变”物理量,想必会给接下来构建相对论时空观的数学表述带来不少方便。
——在洛伦兹变换前后寻找不变量?这似乎并不容易,毕竟在洛伦兹变换下,连“长度”和“时间”在不同参考系里都能呈现出不同的样貌!显然这两者都不是我们要追寻的不变量。但是,洛伦兹变换里空间坐标和时间坐标“你中有我、我中有你”的特点,让我们想到了三维空间里一个很类似的行为——旋转!不妨让我们先回过头去研究下三维空间里的坐标旋转变换,说不定能为我们提供一些其实。
◆ “旋转”中的不变性:三维空间中的标量、矢量与张量
考虑三维空间里的一个点\mathrm{P}——简化起见,我们将它放在\mathrm{S}系的z=0平面上,所以在\mathrm{S}系里测得它的空间坐标为\left( x,y,0 \right) 。现在,假设原本站在\mathrm{S}系原点处的观测者逆时针方向扭头了\phi 角(转轴方向垂直于z轴),得到了一个新的参考系\mathrm{S}^{'}系(\mathrm{S}系和\mathrm{S}^{'}系的原点都重合),在\mathrm{S}^{'}系里测得的点\mathrm{P}空间坐标为\left( x^{'},y^{'},0 \right) 。试问:\left( x,y,0 \right) 和\left( x^{'},y^{'},0 \right) 之间满足什么关系?
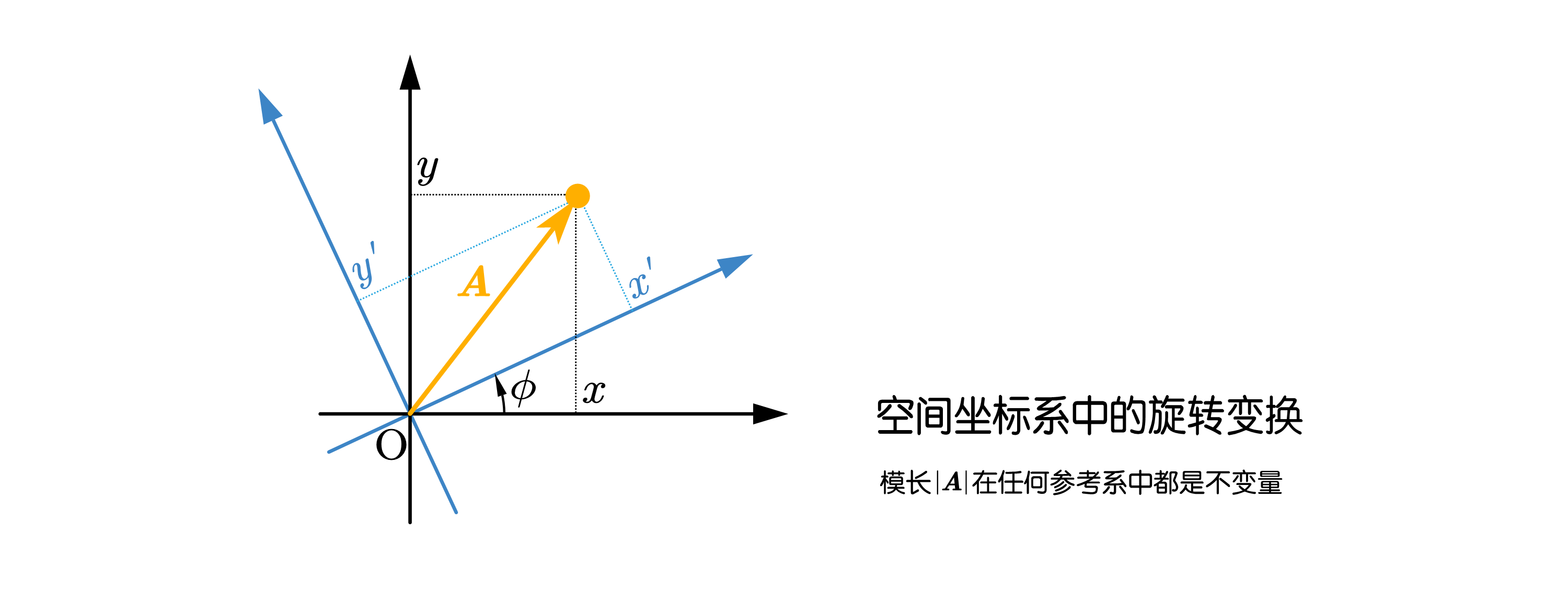
这当然不是个多难的问题,它的答案在第一篇就已经揭晓,稍微画个图就可以写出下面的关系式:
\begin{cases} x^{'}=x\cos \phi +y\sin \phi\\ y^{'}=-x\sin \phi +y\cos \phi\\ z^{'}=z\\\end{cases}\\
或者写成矩阵:
\left[ \begin{array}{c} x^{'}\\ y^{'}\\ z^{'}\\ \end{array} \right] =\left[ \begin{matrix} \cos \phi& \sin \phi& 0\\ -\sin \phi& \cos \phi& 0\\ 0& 0& 1\\ \end{matrix} \right] \left[ \begin{array}{c} x\\ y\\ z\\ \end{array} \right]\\
——将两个参考系里测得\mathrm{P}点的空间坐标矢量分别用\boldsymbol{x}和\boldsymbol{x}^{'}表示,而这个表示旋转的矩阵记作\mathbf{R},它就可以写作:
\boldsymbol{x}^{'}=\mathbf{R}\boldsymbol{x}\\
——以上都没有什么问题。而且我们知道,如果将\phi 换成-\phi ,则\boldsymbol{x}^{'}便可以再旋转回到\boldsymbol{x}。
现在我们希望寻找到这个坐标旋转变换过程中的“不变量”,初看起来有点难找——这坐标系一转动,x方向和y方向的分量都发生了变化呀。但别急,我们很快就能发现——无论坐标系怎样旋转,这个\mathrm{P}点到原点之间的距离长度(也可以说是\boldsymbol{x}这个矢量的“总模长”,暂且写成\left| \boldsymbol{x} \right|吧)是不会改变的。也就是说,有一个不变量在不同参考系里保持不变:
|\boldsymbol{x}|=\sqrt{x^2+y^2+z^2}=\sqrt{{x^{'}}^2+{y^{'}}^2+{z^{'}}^2}=|\boldsymbol{x}^{'}|\\
——这个不变关系也可以由上述的坐标变换公式进行证明。
【符号说明】我们再次强调下这里的符号约定。矢量\boldsymbol{x}在整个电动力学篇章里都表示整个空间坐标,即\left(x,y,z\right),或者说\boldsymbol{x}=x\boldsymbol{e}_x+y\boldsymbol{e}_y+z\boldsymbol{e}_z,其意义就等同于在经典力学篇章我们熟悉的\boldsymbol{r}(而不单单只代指x方向的矢量)。所以这里\boldsymbol{x}的“模长”其实就是原来的r,只不过为了避免混淆,不直接用x,而用|\boldsymbol{x}|表示。 顺便我们还可以发现:正是因为要维持这种“模长”的不变性,所以对变换矩阵\mathbf{R}的一些性质也提出了要求。维持\left| \boldsymbol{x} \right|不变就相当于维持\left| \boldsymbol{x} \right|^2不变。由于|\boldsymbol{x}|^2=\boldsymbol{x}\cdot \boldsymbol{x}、|\boldsymbol{x}^{'}|^2=\boldsymbol{x}^{'}\cdot \boldsymbol{x}^{'},因此可以看出:
|\boldsymbol{x}^{'}|^2=\boldsymbol{x}^{'}\cdot \boldsymbol{x}^{'}=\left( \mathbf{R}\boldsymbol{x} \right) \cdot \left( \mathbf{R}\boldsymbol{x} \right) =\boldsymbol{x}\cdot \boldsymbol{x}=|\boldsymbol{x}|^2\\
——利用爱因斯坦求和约定有x_{i}^{'}=R_{ij}x_j,因此上述“模长不变”的条件可以写成:
x_{i}^{'}x_{i}^{'}=R_{im}x_mR_{in}x_n=x_ix_i\\
——将右边x_ix_i写作\delta _{mn}x_mx_n,则立刻可以推出R_{im}R_{in}=\delta _{mn}。如果用矩阵形式写出,记\mathbf{R}^{\mathrm{T}}为\mathbf{R}的转置矩阵,那么一定有矩阵元R_{im}=R_{mi}^{\mathrm{T}}。对于R_{mi}^{\mathrm{T}}R_{in}=\delta _{mn},用矩阵符号写出有:
\mathbf{R}^{\mathrm{T}}\mathbf{R}=\mathbf{1}\\
——其中\mathbf{1}为单位矩阵,这意味着\mathbf{R}^{\mathrm{T}}=\mathbf{R}^{-1},即\mathbf{R}的转置矩阵等于它的逆矩阵,这样的矩阵也称作正交矩阵。因此,\mathbf{R}是正交矩阵是它能够保证“模长”在变换前后不变的充分必要条件,也就是说只有正交矩阵才可能用来表示刚性坐标架的旋转。
为什么我们要讨论坐标系的旋转呢?本质上是为了将物理量分为标量、矢量、张量等类型。这些分类在我们以前就很熟悉,但往往只是基于直观,现在我们可以用坐标系下的变换方式作为基础,对以上概念进行严谨的定义:
标量:如果物理量没有任何空间取向关系,仅用一个分量就能描述(不需要指标,记作T),在任何坐标系旋转下这些量的值都不会改变(T^{'}=T),则称它为标量或零阶张量,例如质量、电荷或温度等。上面的\left| \boldsymbol{x} \right|就是个标量,正因如此它才能在坐标系的旋转前后永不改变。——注意这里我们对标量的定义是比较严格的,将“标量”作为是“不变量”的同义词。矢量的个别分量(例如v_x)以前我们也把它叫做标量,但它显然不符合我们如今的定义,因为它并不能保证旋转坐标系后保持自身不变。
矢量:如果物理量在空间里有一定的取向性,需要用三个分量描述(需要一个指标,记作T_i),这三个分量在坐标系的旋转下改变的方式和之前坐标\boldsymbol{x}改变的方式一致(即T_{i}^{'}=R_{ij}T_j),则称它为矢量或一阶张量,例如速度或电场、磁场等。
有个别微分算符也具有矢量性质,例如我们熟悉的\mathbf{\nabla }算符,它在\mathrm{S}系里的分量可以写作\frac{\partial}{\partial x_i},在\mathrm{S}^{'}系里的分量则可写作\frac{\partial}{\partial x_{i}^{'}},也满足\frac{\partial}{\partial x_{i}^{'}}=\frac{\partial x_j}{\partial x_{i}^{'}}\frac{\partial}{\partial x_j}=R_{ij}\frac{\partial}{\partial x_j}的关系,所以\mathbf{\nabla }算符也可以说是一个矢量算符。
张量:如果物理量在空间里有更复杂的取向性,需要用九个分量描述(需要两个指标,记作T_{ij}),在坐标系旋转时每一个指标都像坐标一样变换(即T_{ij}^{'}=R_{im}R_{jn}T_{mn}),则称二阶张量,例如转动惯量、应力或电磁场的动量流密度等。以此类推还可以定义更高阶的张量。
——在这样的分类下,我们可以更好地考虑物理规律是否与坐标轴转动的取向无关的问题。例如牛顿第二定律\boldsymbol{F}=m\ddot{\boldsymbol{x}},其中\boldsymbol{F}和\ddot{\boldsymbol{x}}都是矢量,它们在坐标轴旋转时按相同的规律变化,m则是标量,无论怎样旋转坐标轴都不会改变。因此在旋转坐标轴后也能保持\boldsymbol{F}^{'}=m^{'}\ddot{\boldsymbol{x}}^{'}的形式不变,即牛顿第二定律与坐标轴取向无关。
◆ 间隔不变性:光速不变原理的数学表述
为什么我们要大动干戈地来研究三维空间里坐标系的旋转?这并不偏题。因为我们只需要将上面给出的三维空间里坐标系旋转的表达式与洛伦兹变换的表达式放在一起对比:
\begin{eqnarray}&&\begin{cases} x^{'}=\cos \phi \cdot x+\sin \phi \cdot y\\ y^{'}=-\sin \phi \cdot x+\cos \phi \cdot y\\ z^{'}=z\\\end{cases}\\& &\begin{cases} x^{'}=\gamma \cdot x-\gamma u\cdot t\\ y^{'}=y\\ z^{'}=z\\ t^{'}=-\gamma u/c^2\cdot x+\gamma \cdot t\\\end{cases}\end{eqnarray}\\
——你会发现这两者出奇相似!别看洛伦兹变换关联了时间和空间,看上去神神叨叨的,但它本质上似乎和三维空间里坐标系旋转这个非常朴素的参考系改变没有什么特别本质的区别。无非就是……你是在\left( x,y \right) 平面上旋转了一下,我是在\left( x,t \right) “平面”上“旋转”了一下而已。
瞬间我们就醒悟过来——洛伦兹变换的图景其实非常清晰。假设我们面前有一栋房子,从不同角度去观察这栋房子,可能有时看到它的正面露出得多一点,有时则看到它的侧面露出得多一点,但我们不会认为这是因为房子本身发生了什么变化(房子的形状尺寸都是固定的),这种变化只源于我们的观察角度(参考系)不同。如果换到坐标系旋转的例子里来说,就是对一根同样长度为l的线段,在不同角度的参考系里有时x方向的分量会大一些、有时y方向的分量会大一些,但我们都知道不管视角怎么变,都有一些“本质”的东西——比方说长度l是固定不变的。同理,我们是不是也可以说:之前那些恼人的“钟慢”、“尺缩”,看上去时间间隔和空间间隔都会随着视角(参考系)的不同变来变去,但其实所谓的“时间”和“空间”都只像房子的“正面”和“侧面”一样,只是同一个事物“本质”所具有的两个不同方面?这个“本质”是不随视角而改变的,只是在有些人的视角里显得“时间”的成分多一些,而另一些人的视角里显得“空间”的成分多一些罢了。
——没错,所以我们接下来就是寻找能够统一时间和空间的不变的“本质”!正如同之前我们发现三维空间里的距离(或者说矢量的模长)在坐标系旋转变换前后不会改变一样,现在我们也要找到一个能在洛伦兹变换前后保持不改变的量,而这个量你或许已经心有所属——它便是我们之前定义的“时空间隔”\Delta s!想来也对,要说把“时间间隔”\Delta t和“空间间隔”\Delta x混搭整合起来,使得\Delta x和\Delta t都成为它的不同侧面(分量),\Delta s自是最合适不过了。
但先别急,我们先要证明\Delta s在洛伦兹变换前后确实是保持不变的——也就是洛伦兹变换前后满足“间隔不变性”。而这自然难不倒我们,只需代入便是。为了方便,我们计算\Delta s的模方\left( \Delta s \right) ^2,根据定义和洛伦兹变换,不难写出:(别忘了\gamma ^2\left( 1-u^2/c^2 \right) =1)
\begin{eqnarray}\left( \Delta s^{'} \right) ^2&=&\left( \Delta x^{'} \right) ^2+\left( \Delta y^{'} \right) ^2+\left( \Delta z^{'} \right) ^2-c^2\left( \Delta t^{'} \right) ^2\\&=&\gamma ^2\left( \Delta x-u\Delta t \right) ^2+\left( \Delta y \right) ^2+\left( \Delta z \right) ^2-c^2\gamma ^2\left( \Delta t-u\Delta x/c^2 \right) ^2\\&=&\gamma ^2\left( 1-u^2/c^2 \right) \left( \Delta x \right) ^2+\left( \Delta y \right) ^2+\left( \Delta z \right) ^2-\gamma ^2\left( 1-u^2/c^2 \right) c^2\left( \Delta t \right) ^2\\&=&\left( \Delta x \right) ^2+\left( \Delta y \right) ^2+\left( \Delta z \right) ^2-c^2\left( \Delta t \right) ^2\\&=&\left( \Delta s \right) ^2\end{eqnarray} \\
——漂亮!因此我们得出的结论是:洛伦兹变换前后,时空间隔\Delta s为不变量,即在所有惯性系下测得的时空间隔\Delta s都相同。由此可见,间隔\Delta s才是时空中那个不变的“本质”,而我们眼中一会儿钟慢,一会儿尺缩,其实都不足为奇,无非是因为我们往往只盯着它的某一个侧面罢了。
从物理意义上来讲,在不同惯性系中保持间隔\Delta s不变,是洛伦兹变换维持光速不变性的必然要求。或者换句话来说:间隔不变性就是光速不变原理的数学表述。
◆ 闵可夫斯基空间
如上所述,在洛伦兹变换下的不变量是间隔\Delta s=\sqrt{\left( \Delta x \right) ^2+\left( \Delta y \right) ^2+\left( \Delta z \right) ^2-c\left( \Delta t \right) ^2}=\sqrt{\left( \Delta r \right) ^2-c\left( \Delta t \right) ^2},\Delta s的地位恰似三维时空中的“距离”\Delta r。由此,我们完全可以将“间隔”\Delta s看作是四维时空里定义出来的一种新的“距离”。有了这个不变量的存在,闵可夫斯基就能构筑起他的四维时空。
别急,还差最后一步!我们通常所说的四维时空坐标用\left( x,y,z,t \right) 表示,但按照通常的欧几里得空间结构,如果我们单单拿这四个量去当坐标的话,这样定义出来的“距离”应该是:
\sqrt{\left( \Delta x \right) ^2+\left( \Delta y \right) ^2+\left( \Delta z \right) ^2+\left( \Delta t \right) ^2}=\sqrt{\left( \Delta r \right) ^2+\left( \Delta t \right) ^2}\\
——并不是\Delta s!显然,这里存在两个问题:第一,时间和空间的量纲不一致,因此并不能放在同一个矢量中,硬要放的话必须补一个常系数c;第二,\Delta s的定义中各项前面的符号有正有负,这和我们通常理解的欧几里得空间稍有不同。
为了解决这两个矛盾,我们需要换用一组新的坐标——其中,为了凑出\left( \Delta t \right) ^2项前的负号,唯一的办法是:将时间坐标改写成虚数!不难发现,如果我们拿\left( x,y,z,\mathrm{i}ct \right) 这四个量分别作为四个时空坐标,这样算出来的四维“距离”才真正是我们所需要的“间隔”\Delta s,即:
\Delta s=\sqrt{\left( \Delta x \right) ^2+\left( \Delta y \right) ^2+\left( \Delta z \right) ^2+\left( \mathrm{i}c\Delta t \right) ^2}=\sqrt{\left( \Delta r \right) ^2-c^2\left( \Delta t \right) ^2}\\
——这便是著名的闵可夫斯基空间的定义,也称作闵可夫斯基四维时空。它用四维坐标\left( x,y,z,\mathrm{i}ct \right) 描述时空的性质,整个时空依然是平直的,所以可以套用欧几里得空间里熟悉的结论。这样,每一个事件在闵可夫斯基空间中可以用一个点来表达(也叫时空点),而事件随时间的演化则在闵可夫斯基空间里划出一条轨迹(也叫世界线),即便是在不同的参考系下两事件的时空间隔\Delta s也不会改变。后面我们会发现:闵可夫斯基空间真正标志了“时间”与“空间”成为了一个不可分割的整体。这一数学形式的发明,是相对论发展历程上的重要里程碑。

◆ 间隔的三种类型与物理意义
在闵可夫斯基空间里,让我们继续来查考时空间隔\Delta s的物理意义。需要注意,由于\left( \Delta s \right) ^2=\left( \Delta r \right) ^2-c^2\left( \Delta t \right) ^2,因此和三维空间里的“距离”平方\left( \Delta r \right) ^2必然为正不同,“时空间隔”的平方\left( \Delta s \right) ^2在不同的情况下可正可负,进而\left( \Delta s \right) 既可能是实数也可能是虚数!根据这一差异,我们可以将两事件之间的\Delta s分为如下三种情况考虑:
类时间隔:如果两事件的间隔满足\left( \Delta s \right) ^2<0,即\Delta s为虚数,我们说该间隔是“类时”的。这是因为此时有\left( \Delta r \right) ^2<c^2\left( \Delta t \right) ^2 ,意味着这两个事件的间隔主要体现在发生时间上的先后差异,至于空间位置的差异反而是次要方面了。举个例子,事件“射箭”和事件“中靶”之间的间隔就属于类时间隔。
什么叫“空间距离是次要的”?对于类时间隔,我们总能找到某个惯性系使得两个事件看上去似乎发生在同一地点(\Delta r=0),这样空间上的距离就被干脆抹平了。(还是拿“射箭”和“中靶”的例子,其实只要永远取和箭相对固定的参考系,就能保证“射箭”和“中靶”两个事件发生在参考系里的同一地点。)但是我们永远不可能找到某个惯性系去使得两个事件看上去发生在同一时间(\Delta t=0),时间上的先后次序差异是抹不掉的!显然我们可以发现:两事件之间若是类时间隔,则这两个事件之间便可以有因果性相联系。(例如这个例子里,“射箭”就是“中靶”的原因,所以不管怎么看都必然要求先“射箭”再“中靶”,正如之前所说的,对于有因果关系联系的事件,其先后次序不可以被逆转)。
——需要补充的是,因果性只是“可以有”,没说“必须有”(比如:“凌晨0:00寝室熄灯”和“凌晨0:10寝室窗外树上的苹果掉下来”这两件事情之间也是类时间隔,但没有因果性。)在这里我们只是强调一种理论上的可能。
类空间隔:如果两事件的间隔满足\left( \Delta s \right) ^2>0,即\Delta s为非零实数(默认取正数),我们说就该间隔是“类空”的。和之前相反,此时有\left( \Delta r \right) ^2>c^2\left( \Delta t \right) ^2,也就是说这两个事件的间隔主要体现在空间位置上的距离,至于时间先后的差异则是次要的。举个例子,事件“凌晨0:00寝室熄灯”和事件“凌晨0:10一艘探测器掠过冥王星”两个之间的间隔就属于类空间隔。
对于这类“时间距离是次要的”情况,我们总能找到某个惯性系使得两个事件看上去似乎发生在同一时间(\Delta t=0)来抹除时间距离差异(甚至可以颠倒时间的先后次序),但是我们永远不可能找到某个惯性系去使得两个事件看上去发生在同一地点(\Delta r=0)。由于光速是信息传递的上限,而这两个事件之间连用光信号联系都办不到,所以:两事件之间若是类空间隔,则这两个事件之间完全不可能有任何因果性的联系。
类光间隔:最后考虑两事件的间隔\left( \Delta s \right) ^2=0的临界情况,此时\Delta s=0,两个事件之间若有想什么因果联系便只有用光信号这一种选择,所以我们说该间隔是“类光”的。显然“类光间隔”是上述两种间隔之间的分界线。
【说明】如果用另一种定义\Delta s=\sqrt{c^2\left( \Delta t \right) ^2-\left( \Delta r \right) ^2},则所有结论会反过来:\left( \Delta s \right) ^2>0为类时间隔、\left( \Delta s \right) ^2<0为类空间隔、\left( \Delta s \right) ^2=0为类光间隔,但显然这并不会对理解带来多少额外的障碍。 ◆ 过去、现在、未来、光锥之外
如果将“现在”某事件取成四维的闵可夫斯基空间的原点,再取所有\left( \Delta s \right) ^2\le 0点的集合,我们将得到沿着时间轴方向上下两个圆锥形对顶而立的形状,这就是所谓的光锥。只有位于光锥之内的事件(与观测者之间是类时或者类光间隔),才是能与“现在”的我们发生因果关系的事件,也是我们所有能感知到的事件。

“光锥”由上下两个圆锥体构成,它们分别代表了所有“能对现在的我们施加因果性影响”的事件(“绝对过去”)和所有“现在的我们能够对其施加因果性影响”的事件(“绝对未来”)。“未来光锥”里的事件正在离我们而去,“过去光锥”里的事件正在以光速向我们奔驰而来——即便你还没有感知到,那些“已经发生”的事件终将影响到我们,“过去光锥”里的一切决定了我们现在的样子,这便是“光锥之内就是命运”的涵义。宇宙间存在着光速这一极限,很多科学家认为我们头顶的参宿四(一颗约600光年外的红超巨星)即将超新星爆发甚至说是已经超新星爆发,但由于我们能看到的永远只是它历史上的影像、是它600年前发出的光,即使它现在已经爆炸了,这个信息我们也要几百年后才能得知。到那时我们也才能看到这个“过去光锥”中既定的“命运”。
而相反,在光锥之外的广袤区域,由于\left( \Delta s \right) ^2>0(与观测者之间是类空间隔),光速的速度极限决定了这里的任何事件都无法对我们施加影响,我们也无法对它们施加任何影响——这是一个我们完全无法进入、完全无法得知的巨大时空区域,它对我们来说,既不是能回忆的过去、也不是能期盼的未来、更不是能感知的现在,而是绝对未知的“光锥之外”(“绝对远离”)。我们的宇宙就有很大一部分藏在光锥之外,或许那部分的宇宙中也有许多重大的事件在发生,或许那些事件也以光速向我们飞来,但只是因为它在我们的光锥之外,这注定了我们无法以任何手段探知或影响它,很无奈,我们只能直接认定那些事件“不存在”或者说“根本没有发生过”了。
这便是狭义相对论光速极限为我们揭示的宇宙图景——光锥之外,一无所知;光锥之内,无处可逃。
<hr/>【二】构建四维协变量
◆ 四维坐标
闵可夫斯基空间里,时间和空间构成了一个不可分割的整体。时空的洛伦兹变换被理解为闵可夫斯基空间里的“旋转”操作,而洛伦兹变换前后维持不变的时空间隔\Delta s便是闵可夫斯基空间中的“模长”——这是完全自洽的,因为“模长”当然不会因为视角的旋转而改变!由此,我们自然能想到在这个四维的闵可夫斯基空间里定义四维的标量、矢量与张量,它们的坐标变换服从和三维空间里的旋转变换完全一样的规律。这些四维的量被称作四维协变量,它是三维空间里标量、矢量与张量的自然推广。利用它们,我们能将四维时空里的物理规律写成更加紧凑的形式。
我们第一个能想到的四维协变量显然是四维空间里的“时空坐标”,显然它应当是一个四维矢量。定义四维坐标\boldsymbol{\tilde{x}}=\left( x,y,z,\mathrm{i}ct \right) ,为了强调它是个四维量我们特地给它的头顶标上波浪线。它同时包含了时间和空间位置两方面的信息,其中前三个坐标分量是空间坐标(x_1=x、x_2=y、x_3=z),第四个坐标分量则是新引入的“虚数”时间坐标(x_4=\mathrm{i}ct),我们也可以将它写成\left( \boldsymbol{x},\mathrm{i}ct \right) 。这样一来,与坐标原点之间的时空间隔\Delta s就可以写为:
\begin{eqnarray}\left( \Delta s \right) ^2&=&x^2+y^2+z^2-c^2t^2\\&=&x_{1}^{2}+x_{2}^{2}+x_{3}^{2}+x_{4}^{2}=\text{不变量}\end{eqnarray}\\
——完全回到了和平常三维时空几乎一模一样的“模长”定义形式!当然,由于对矢量求模方其实就等于点乘自己(\boldsymbol{\tilde{x}}\cdot \boldsymbol{\tilde{x}}),利用爱因斯坦符号约定,还可以写为:
\left( \Delta s \right) ^2=x_{\mu}x_{\mu}=\text{不变量}\\
——它是四维时空里的标量(四维标量,而“标量”意味着是其实就是不变量),也就是即便换到另一个坐标系里,也会有x_{\mu}x_{\mu}=x_{\mu}^{'}x_{\mu}^{'}。这里下标的\mu 和以前所用的i、j、k等等是一样的,也是指标的代号,只是对于四维量的指标我们一般用希腊字母,以与使用拉丁字母的三维量指标相区别。换句话直说就是:如果遇到i这样的拉丁字母指标,就用1\sim 3遍历代入;如果遇到\mu 这样的希腊字母指标,就用1\sim 4遍历代入。
◆ 洛伦兹变换的四维形式:四维时空里的旋转
当我们定义了四维的坐标矢量后,我们就可以把洛伦兹变换从形式上看成是在四维空间里的“旋转”。类比于之前的旋转矩阵\mathbf{R},我们显然可以定义出对应于洛伦兹变换的旋转矩阵\mathbf{\tilde{L}}。
我们先模仿旋转矩阵\mathbf{R}写出洛伦兹变换矩阵\mathbf{\tilde{L}}。由于我们假设的参考系相对运动方向沿着x轴,也就是说会改变的仅有x方向和\mathrm{i}ct方向,而y方向和z方向并不受影响,所以暂时可以先把\mathbf{\tilde{L}}写成:
\mathbf{\tilde{L}}=\left[ \begin{matrix} \cos \phi& 0& 0& \sin \phi\\ 0& 1& 0& 0\\ 0& 0& 1& 0\\ -\sin \phi& 0& 0& \cos \phi\\ \end{matrix} \right] \\
——这里表示“旋转角度”的\phi 并没有物理上可观测到的意义,我们的目的仅仅是把它的形式找出来。
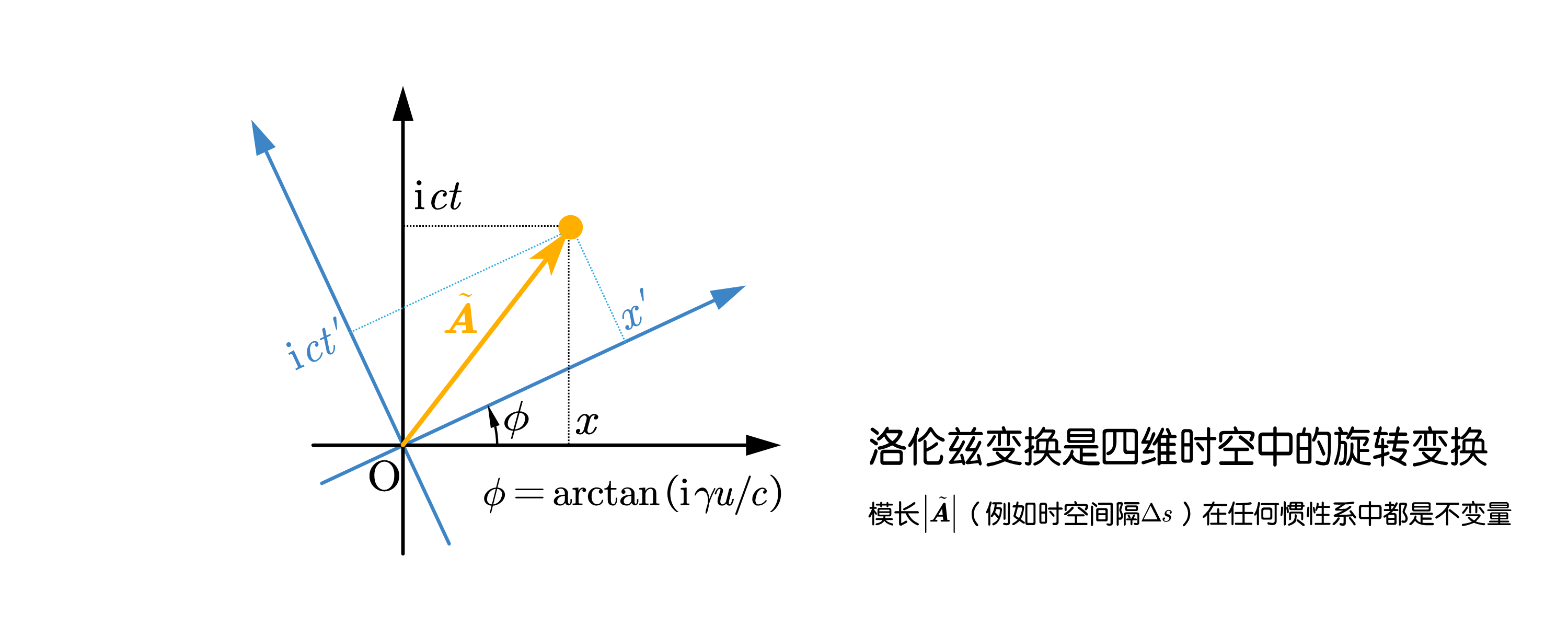
显然\phi 唯一可能关联的量只有两个参考系之间的相对速率u。和我们之前推导洛伦兹变换的方法一样:所有在\mathrm{S}^{'}系中是静止的点(换句话说就是空间坐标x_{1}^{'}始终固定),在\mathrm{S}系里看来都是在以速度u运动,即\frac{\mathrm{d}x_1}{\mathrm{d}t}=u,或者说\frac{\mathrm{d}x_1}{\mathrm{d}x_4}=\frac{u}{\mathrm{i}c}(别忘了x_4=\mathrm{i}ct)。那么,按照四维时空里的几何关系,我们可以画一条“等x_{1}^{'}线”,观察它在\mathrm{S}系里的斜角,立刻就可以写出:
\frac{\mathrm{d}x_1}{\mathrm{d}x_4}=-\tan \phi \\
于是:
\tan \phi =\frac{\mathrm{i}u}{c}\\
——所以\cos \phi =\gamma 、\sin \phi =\mathrm{i}\gamma u/c。代入我们已经画好的旋转矩阵\mathbf{\tilde{L}},就能得到它的形式:
\mathbf{\tilde{L}}=\left[ \begin{matrix} \gamma& 0& 0& \mathrm{i}\gamma u/c\\ 0& 1& 0& 0\\ 0& 0& 1& 0\\ -\mathrm{i}\gamma u/c& 0& 0& \gamma\\ \end{matrix} \right] \\
这个矩阵\mathbf{\tilde{L}}也叫洛伦兹矩阵,显然它满足正交矩阵的性质,所以它确实能够充当一个表示“旋转”意义矩阵。从张量的角度上来说,\mathbf{\tilde{L}}也可以说成是定义在闵可夫斯基空间里的一个二阶张量,即四维张量,它和三维空间里其他普通的二阶张量具备完全相同的性质。进一步我们还要指出:\mathbf{\tilde{L}}也要满足像三维空间里的矩阵\mathbf{R}一样的性质,也就是说它必须是一个正交矩阵才能用于描述“旋转”,而这一点很容易验证,它也满足L_{\lambda \mu}L_{\lambda \nu}=\delta _{\mu \nu},即\mathbf{\tilde{L}}^{\mathrm{T}}\cdot \mathbf{\tilde{L}}=\mathbf{1}。
这样一来,整个洛伦兹变换就可以写成如下的四维形式:
\left[ \begin{array}{c} x^{'}\\ y^{'}\\ z^{'}\\ \mathrm{i}ct^{'}\\ \end{array} \right] =\left[ \begin{matrix} \gamma& 0& 0& \mathrm{i}\gamma u/c\\ 0& 1& 0& 0\\ 0& 0& 1& 0\\ -\mathrm{i}\gamma u/c& 0& 0& \gamma\\ \end{matrix} \right] \left[ \begin{array}{c} x\\ y\\ z\\ \mathrm{i}ct\\ \end{array} \right] \\
即:
\boldsymbol{\tilde{x}}^{'}=\mathbf{\tilde{L}}\boldsymbol{\tilde{x}}\\
或者写成:
x_{\mu}^{'}=L_{\mu \nu}x_{\nu}\\
——我们用几何方法再次推导出了洛伦兹变换!和此前已知的洛伦兹变换表达式相比,很容易发现它们完全一致。由此,我们再次坚定了一个信念:惯性系中的时空转换可以用闵可夫斯基空间中的“旋转”来刻画。
◆ 四维速度
定义了四维坐标,我们自然就会试图去定义其他的四维矢量,例如四维速度、四维加速度等。
初看起来,速度不就等于坐标对时间求导嘛!所以我们很容易直接将四维速度定义成\boldsymbol{\tilde{v}}=\frac{\mathrm{d}\boldsymbol{\tilde{x}}}{\mathrm{d}t}。但这样定义的问题在于:在进行洛伦兹变换时,\mathrm{d}\boldsymbol{\tilde{x}}作为四维矢量按四维矢量的规则“旋转”,但\mathrm{d}t却不是一个固定不变的四维标量(它在洛伦兹变换时自己会变的),所以整体\boldsymbol{\tilde{v}}并不能按四维矢量的规则“旋转”!所以,要定义出一个真正靠谱的四维速度矢量,我们便不能拿\mathrm{d}\boldsymbol{\tilde{x}}去随便除一个\mathrm{d}t,而要除以一个真正能维持不变(是四维标量)的“时间”才行。
什么叫“不变的时间”呢?我们联想了上一篇中提到的“固有时”\Delta \tau (当然它在取微分的时候要写成\mathrm{d}\tau 了)。简单来说,固有时相当于用“在自己参考系里看自己”计时得到的时间,或者说是自己身边携带的时钟上显示的时间——这显然是在任何参考系里都维持不变的,所以它就是我们要找的四维标量。(也可以尝试用间隔不变性去证明。)别忘了“钟慢公式”\mathrm{d}t=\gamma \mathrm{d}\tau ,我们可以利用\mathrm{d}\tau 去代替\mathrm{d}t,定义出的“四维速度”:
\boldsymbol{\tilde{U}}=\frac{\mathrm{d}\boldsymbol{\tilde{x}}}{\mathrm{d}\tau}=\left( \gamma v_x,\gamma v_y,\gamma v_z,\mathrm{i}c\gamma \right) \\
——即\boldsymbol{\tilde{U}}=\left( \gamma \boldsymbol{v},\mathrm{i}c\gamma \right) ,这里的\boldsymbol{\tilde{U}}才是我们真正要找的四维速度矢量!注意它的第四个分量是个常量。而作为一个四维矢量,它的模方必然也是个四维标量(不变量),这是可以证明的,它的模方显然是:
\left| \boldsymbol{\tilde{U}} \right|^2=\gamma ^2\left( v^2-c^2 \right) =-c^2=\text{不变量}\\
当我们真正来描述物体运动的速度时,\boldsymbol{\tilde{U}}显然是不如\boldsymbol{v}直观的,但为什么我们偏爱于使用它呢?那是因为在四维空间里计算时\boldsymbol{\tilde{U}}能够彻底按照矢量的规则进行变换。举个例子,在考察不同参考系下的速度时,如果使用四维速度矢量\boldsymbol{\tilde{U}},它作为四维时空里一个“普普通通”的矢量,直接用洛伦兹变换“旋转”一下就可以解决,也就是可以满足:
U_{\mu}^{'}=L_{\mu \nu}U_{\nu}\\
——你当然也可以写成\boldsymbol{\tilde{U}}^{'}=\mathbf{\tilde{L}}\boldsymbol{\tilde{U}},不过未来我们可能更加亲睐这些带指标的分量式写法。如果再具体展开来写,就是:
\left[ \begin{array}{c} \gamma v_{x}^{'}\\ \gamma v_{y}^{'}\\ \gamma v_{z}^{'}\\ \mathrm{i}c\gamma\\ \end{array} \right] =\left[ \begin{matrix} \gamma& 0& 0& \mathrm{i}\gamma u/c\\ 0& 1& 0& 0\\ 0& 0& 1& 0\\ -\mathrm{i}\gamma u/c& 0& 0& \gamma\\ \end{matrix} \right] \left[ \begin{array}{c} \gamma v_x\\ \gamma v_y\\ \gamma v_z\\ \mathrm{i}c\gamma\\ \end{array} \right] \\
——和普通的坐标矢量变换一模一样。相反,如果坚持使用\boldsymbol{v},我们都知道这时的速度变换式就成了:
\begin{cases} v_{x}^{'}=\dfrac{v_x-u}{1-uv_x/c^2}\\ v_{y}^{'}=\dfrac{v_y}{\gamma \left( 1-uv_x/c^2 \right)}\\ v_{z}^{'}=\dfrac{v_z}{\gamma \left( 1-uv_x/c^2 \right)}\\\end{cases}\\
——尽管本质相同,但计算起来显得繁琐,形式上也不太好看。你可以尝试验证这两种速度变换形式的等价性。
◆ 四维波矢
接下来让我们讨论下一个被称为四维波矢的四维矢量\boldsymbol{\tilde{k}},听这个名字就知道它一定和电磁波的传播有关。
假设在\mathrm{S}系中有一支角频率为\omega 、波矢为\boldsymbol{k}的电磁波在真空中传播,换到另一个参考系\mathrm{S}^{'}里看,由于“钟慢”“尺缩”等等一系列效应,所测到的新的\omega ^{'}和\boldsymbol{k}^{'}可能和之前都有不同,但在这个变换里是否也存在某些不变的量呢?答案是肯定的。我们知道,无论对电磁波选择电场还是磁场进行表示,它们的波动规律始终正比于一个相位因子\mathrm{e}^{\mathrm{i}\left( \boldsymbol{k}\cdot \boldsymbol{x}-\omega t \right)},或者干脆写成\mathrm{e}^{\mathrm{i}\phi},其中\phi =\boldsymbol{k}\cdot \boldsymbol{x}-\omega t便是电磁波的相位。我们假定让\mathrm{S}系和\mathrm{S}^{'}系在t=t'=0时刻原点重合(\boldsymbol{x}=\boldsymbol{x}'=0),并假定在零时刻刚好观察到电磁波的波峰位于原点,从这时开始直到下一个波峰到达\mathrm{S}系原点,这件事情在\mathrm{S}系看来有t=2\pi /\omega 、\boldsymbol{x}=\mathbf{0}、\phi =-2\pi ,而在\mathrm{S}^{'}中通过洛伦兹变换可以求出这件事的时空坐标分别是t^{'}=2\pi \gamma /\omega 和x^{'}=\gamma \left( x-2\pi u/\omega \right) (这些都和\mathrm{S}系里的结果不一样),但是依旧有\phi ^{'}=\phi =-2\pi !——不难理解,因为某个波峰通过某个时空点是一个纯粹物理事件,而相位仅仅是一个计数的问题,当然不会受到参考系改变的影响。于是我们会得到一个结论:相位\phi 是一个洛伦兹变换中的不变量,或者说是一个四维标量。即:
\phi =\boldsymbol{k}\cdot \boldsymbol{x}-\omega t=\text{不变量}\\
——而我们注意到,空间与时间坐标\left( \boldsymbol{x},\mathrm{i}ct \right) 已经凑成了一个四维矢量\boldsymbol{\tilde{x}}了!由此我们猜想,如果能再将波矢\boldsymbol{k}和频率\omega 再凑成一个四维矢量,嗯不妨就取\left( \boldsymbol{k},\mathrm{i}\omega /c \right) 吧,把它叫做\boldsymbol{\tilde{k}},这样上面的式子就能干脆利落地写成两个四维矢量点乘的形式(\boldsymbol{\tilde{k}}\cdot \boldsymbol{\tilde{x}}),点乘便会自然得到一个四维标量\phi ,这无疑是极为合理的。
于是,我们就“凑出”了“四维波矢”\boldsymbol{\tilde{k}}=\left( k_x,k_y,k_z,\mathrm{i}\omega /c \right) ,它前三个分量描述波矢,第四个分量描述频率。同时还能得到:
\phi =k_{\mu}x_{\mu}=\text{不变量}\\
和四维坐标、四维速度这些四维矢量一样,四维波矢\boldsymbol{\tilde{k}}在参考系间的转换也可以直接利用洛伦兹矩阵\mathbf{\tilde{L}}进行。即k_{\mu}^{'}=L_{\mu \nu}k_{\nu},也就是说它可以直接套入洛伦兹变换式,得到:
\begin{cases} k_{x}^{'}=\gamma \left( k_x-u\omega /c^2 \right)\\ k_{y}^{'}=k_y\\ k_{z}^{'}=k_z\\ \omega ^{'}=\gamma \left( \omega -uk_x \right)\\\end{cases}\\
◆ 四维微分算符
毫不奇怪,三维空间里的算符也能推广到四维。
以三维空间里的矢量微分算符\mathbf{\nabla }为例,它的定义是\mathbf{\nabla }=\left( \frac{\partial}{\partial x},\frac{\partial}{\partial y},\frac{\partial}{\partial z} \right) 。按这个形式,我们能直接写出推广到四维的矢量微分算符,你也可以将它写成\mathbf{\tilde{\nabla}},不过我们更喜欢用\partial _{\mu}表示,它的定义是:
\partial _{\mu}=\frac{\partial}{\partial x_{\mu}}=\left( \frac{\partial}{\partial x}, \frac{\partial}{\partial y}, \frac{\partial}{\partial z}, \frac{1}{\mathrm{i}c}\frac{\partial}{\partial t} \right) =\left( \mathbf{\nabla }, \frac{1}{\mathrm{i}c}\frac{\partial}{\partial t} \right) \\
——可以看出它也有四个分量,前三个分量代表对空间坐标求导,第四个分量代表对时间坐标求导。不难证明它也有和其他四维矢量相同的性质。
作为标量算符的\nabla ^2(拉普拉斯算子)同样可以做此推广。在三维空间里,\nabla ^2=\mathbf{\nabla }\cdot \mathbf{\nabla };在四维空间里,\Box ^2=\partial _{\mu}\partial _{\mu},这个大方框\Box ^2就是推广得到的“四维版”拉普拉斯算子——达朗贝尔算子。即:
\Box ^2=\partial _{\mu}\partial _{\mu}=\nabla ^2-\frac{1}{c^2}\frac{\partial}{\partial t}\\
达朗贝尔算子的引入使得描述电磁波的波动方程变得异常简单,原本是:
\begin{cases} \nabla ^2\boldsymbol{E}-\dfrac{1}{c^2}\dfrac{\partial ^2\boldsymbol{E}}{\partial t^2}=\mathbf{0}\\ \nabla ^2\boldsymbol{B}-\dfrac{1}{c^2}\dfrac{\partial ^2\boldsymbol{B}}{\partial t^2}=\mathbf{0}\\\end{cases}\\
现在直接可以写成:
\begin{cases} \Box ^2\boldsymbol{E}=\mathbf{0}\\ \Box ^2\boldsymbol{B}=\mathbf{0}\\\end{cases}\\
——为啥符号要用一个大方框?笔者不负责任地猜测:这是为了表示这是一个四维时空里的微分算子。采用一个四边形,刚好能和三维空间里三角形的\nabla 保持一致。
【符号说明】有些书上直接用\Box就表示达朗贝尔算子,而不用\Box ^2。 <hr/>【三】四维矢量应用举例
◆ 例1:光行差现象
早在1728年,英国天文学家布拉德雷(第十四章中提及过他发现了地轴的章动)发现:在一年中的不同时间里观察同一颗恒星,其在星空中显现的位置会有非常微小的变化(变化幅度大约在20.5角秒),而这种变化恰好以一年为一个周期。
你或许会认为这种微小差别是恒星视差导致的(因为地球每年绕太阳公转一圈,所以一年中的不同时候与恒星的相对位置会有微小差别,导致视角的微小变化),但即便考虑了恒星视差,也不能完全解释这种周期运动。真正带来这种差异的除了公转带来的观测位置变化外,还有公转速度的周期性变化导致的差异。简而言之,即便是在同一位置观察同一颗恒星,静止参考系中的观察者所观察到的恒星位置和运动参考系里观察到的恒星位置也会有不同,这种差异被称作光行差。——就好比说下雨的时候,站在原地不动的人感觉到雨滴是从正上方落下的,而向前走的人感觉雨滴是从前方倾斜落下的,因此需要把伞微微向前倾斜,走得越快就要把伞倾斜得越厉害。而与下雨不同的是,经典的速度合成公式解释不了涉及到光速的情况,要想真正将光行差现象解释清楚,必须要考虑到相对论效应的存在。
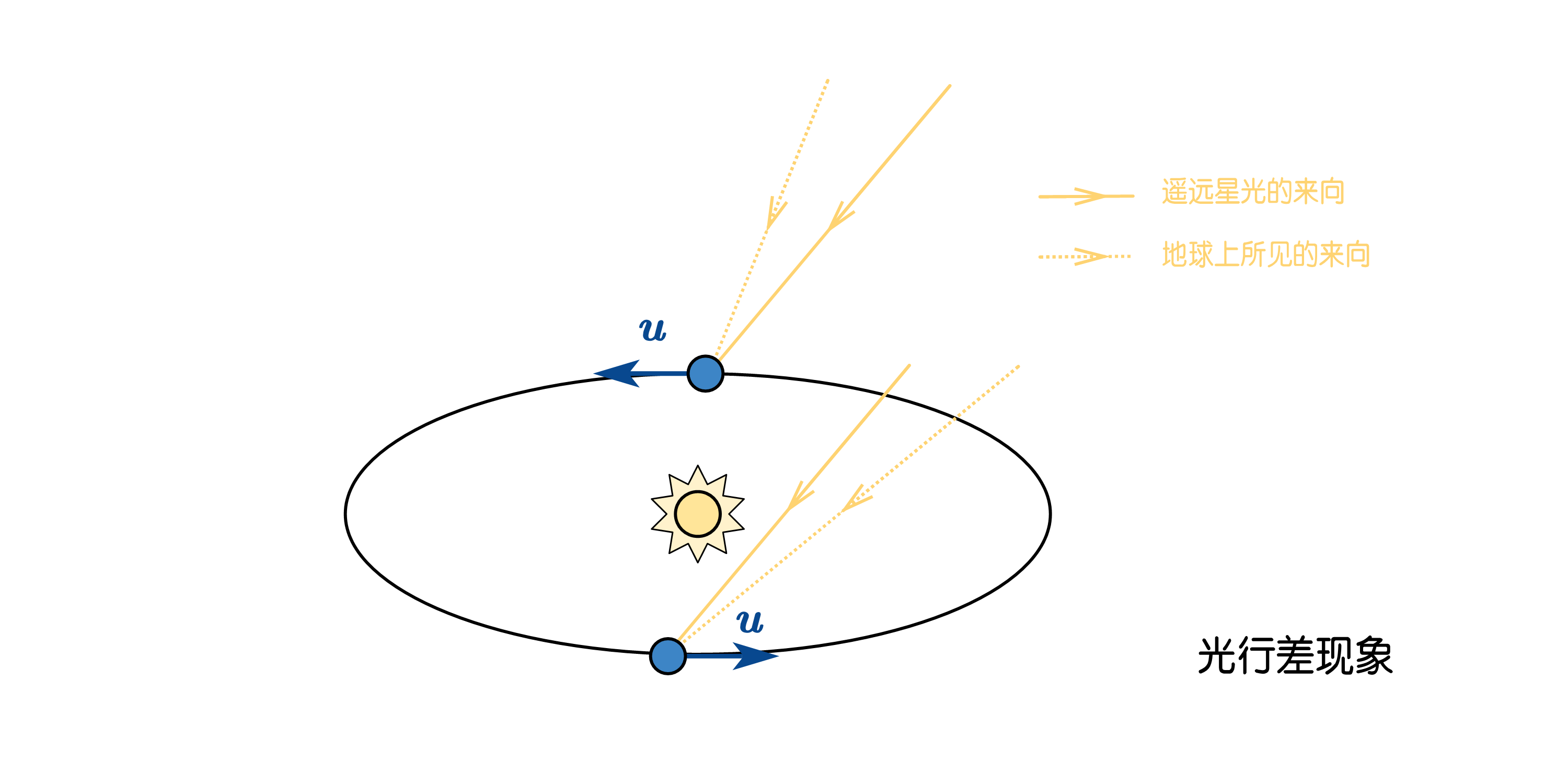
设地球参考系为\mathrm{S},太阳参考系(假设对光源来说属于静系)为\mathrm{S}^{'},两个参考系的原点在某一瞬间重合,两系间的相对速度u(也就是地球公转速度)所朝方向为共同的x方向。假设遥远恒星的星光在\left( x,y \right) 平面内,在\mathrm{S}系看来,星光方向(即\boldsymbol{k}方向)与x轴方向夹角为\theta ;在\mathrm{S}^{'}系看来,星光方向(即\boldsymbol{k}^{'}方向)与x^{'}轴方向夹角为\theta ^{'}。
利用四维波矢满足k_{\mu}^{'}=L_{\mu \nu}k_{\nu},可以写出四维波矢的洛伦兹变换式,如上:
\begin{cases} k_{x}^{'}=\gamma \left( k_x-u\omega /c^2 \right)\\ k_{y}^{'}=k_y\\ k_{z}^{'}=k_z\\ \omega ^{'}=\gamma \left( \omega -uk_x \right)\\\end{cases}\\
根据k_x=k\cos \theta 、k_{x}^{'}=k^{'}\cos \theta ^{'},容易写出:
\begin{cases} k^{'}\cos \theta ^{'}=\gamma \left( k\cos \theta -u\omega /c^2 \right)\\ \omega ^{'}=\gamma \left( \omega -uk\cos \theta \right)\\\end{cases}\\
——要注意,不管那个参考系,总有k=\omega /c成立(即k=\omega /c、k^{'}=\omega ^{'}/c),由此将k与k^{'}全部用\omega 和\omega ^{'}表示出来,得到:
\begin{cases} \omega ^{'}\cos \theta ^{'}=\gamma \left( \omega \cos \theta -u\omega /c \right)\\ \omega ^{'}=\gamma \left( \omega -u\omega \cos \theta /c \right)\\\end{cases}\\
联立消掉\omega ^{'}(留下\omega ,因为\omega 相当于是星光的固有频率)最后得出:
\cos \theta =\frac{\cos \theta ^{'}+u/c}{1+\cos \theta ^{'}u/c}\\
——所以我们发现,\cos \theta 和\cos \theta ^{'}确实有显著差别!为了更进一步计算\theta 与\theta ^{'}的差别究竟有多大,我们求出:
\sin \theta =\sqrt{1-\cos ^2\theta}=\frac{\sin \theta ^{'}}{1+\cos \theta ^{'}u/c}\\
——以上是考虑到u\ll c,也就是u/c为小量,只保留到一阶,二阶小量也就是含有\left( u/c \right) ^2的直接舍弃。于是,\theta 与\theta ^{'}之间的差别就可以写成:
\Delta \theta =\theta ^{'}-\theta \approx \sin \left( \theta ^{'}-\theta \right) =u\sin \theta ^{'}/c\\
——考虑到地球公转的轨道速度大约为u=30 \mathrm{km}/\mathrm{s},在一年中不同时候的u分量最多可相差60 \mathrm{km}/\mathrm{s},一下子就可以算出在地球上可能观察到的最大光行差确实就是20角秒左右!以上结论和光行差现象的观测结果完全一致。光行差现象得到了理论解释,意味着地球的运动、光速的有限性以及狭义相对论理论的可靠性都得到了证实,人们也可以用光行差观测的结果来更精确地测定光速的数值。
◆ 例2:相对论性多普勒效应
光行差现象证明了:在静止参考系和运动参考系中同时观察某个光源,所看到的光源位置(即光的来向)会有不同。除此以外,还有什么现象会不同呢?我们立刻联想到了多普勒效应——光的频率大概也会产生差异吧!再回顾一下声波中的多普勒效应:远方急驶过来的火车鸣笛声变得尖细(即频率变高),而离我们而去的火车鸣笛声变得低沉(即频率变低)。荷兰气象学家拜斯·巴洛特在1845年让一队喇叭手站在一辆从荷兰乌德勒支附近疾驶而过的敞篷火车上吹奏,他在站台上测到了音调的改变,这是科学史上最有趣的实验之一。
光波(电磁波)也是一种波,那么当波源和观察者存在相对运动时,势必也会产生多普勒效应,导致频率的改变。但光的多普勒效应的特点在于:光以光速c传播,所以我们曾经在经典力学里学到的多普勒效应频率公式对于光来说是不适用的,讨论光的多普勒效应必须要考虑到狭义相对论。因此这也被称为相对论性多普勒效应。
好在我们可以利用四维波矢来推导相对论性多普勒效应的频率公式。可以从我们刚刚得到的结论出发,因为有:
\begin{cases} \omega ^{'}\cos \theta ^{'}=\gamma \left( \omega \cos \theta -u\omega /c \right)\\ \omega ^{'}=\gamma \left( \omega -u\omega \cos \theta /c \right)\\\end{cases}\\
将最后一式直接写作:
\omega ^{'}=\gamma \omega \left( 1-u\cos \theta /c \right) =\omega \cdot \frac{1-\left( u/c \right) \cos \theta}{\sqrt{1-\left( u/c \right) ^2}}\\
——这就是相对论性多普勒效应的频率公式。通过静系里的固有频率\omega ,可以直接换算出动系里观测到的频率\omega ^{'}。
我们立刻可以发现相对论性多普勒效应和经典多普勒效应的两大重要差别——第一,相对论性多普勒效应不区分究竟是“光源运动”还是“观察者运动”,这是因为光在真空中就能传播,不需要什么介质,相对论也不承认存在什么“绝对参考系”,所以讨论到底是光源还是观察者相对于“真空”运动是毫无意义的,有意义的只可能是光源和观察者之间的相对运动,只要认准了这个相对速度u,就不需要再作区分(你可以尝试交换公式里所有带撇和不带撇的物理量,再将u改为-u,你会发现公式还是完全一致的)。第二,在相对论性多普勒效应中,\omega ^{'}除了取决于\omega 和u以外,还和光线的来向\theta 有关,改变不同的\theta 将会得到不同的结果。有时,我们更喜欢用在观察者(动系)里测得的光线来向\theta ^{'}代入,这样的频率公式变为:
\omega ^{'}=\frac{\omega}{\gamma \left( 1+u\cos \theta ^{'}/c \right)}=\omega \cdot \frac{\sqrt{1-\left( u/c \right) ^2}}{1+\left( u/c \right) \cos \theta ^{'}}\\
不妨举个例子:若\theta ^{'}=0(\theta ^{'}=0和\boldsymbol{u}同向),意味着观察者是背离光源方向前进,测到的光波频率\omega ^{'}小于固有频率\omega ;若\theta ^{'}=\pi (\boldsymbol{k}^{'}和\boldsymbol{u}反向),意味着观察者是迎着光源方向前进,测到的光波频率\omega ^{'}大于固有频率\omega 。这和经典多普勒效应的结论在定性上一致,也被称作纵向多普勒效应。在这种情况下,相对论性多普勒效应的公式可以简单写成:
\omega ^{'}=\omega \cdot \sqrt{\frac{c-u}{c+u}}\\
——注意u以观测者和波源相对远离为正,相对接近为负。如果u/c\ll 1,公式还可以在泰勒展开后只保留一阶小量,即近似写成\omega ^{'}=\omega \left( 1-\frac{u}{c} \right) ,这其实就是回归到了经典情况。
与经典情况不同的地方在哪呢?考虑\theta ^{'}=\pi /2(\boldsymbol{k}和\boldsymbol{u}垂直),也就是观察者沿着垂直于光来向的方向前进。如果从经典力学理论出发,这种情况是不应该产生任何多普勒频移的(没有径向速度),但在相对论情况下,我们可以计算出这时观测到的频率为:
\omega ^{'}=\frac{\omega}{\gamma}=\omega \sqrt{1-\left( u/c \right) ^2}<\omega \\
——也就是说,观察者测到的光波频率\omega^{'}还是小于固有频率\omega!这种情况称为横向多普勒效应,是相对论效应特有的结果。横向多普勒效应的存在很快也被实验所证实,这也成了相对论理论可靠的证据之一。当u\ll c时,横向多普勒效应展开最高也仅是u/c的二阶小量,这说明横向多普勒效应本身比纵向多普勒效应要小得多,难怪近似到经典情况时可以忽略不计。
法国物理学家菲索于1848年对来自恒星辐射的波长偏移做了解释,指出了利用这种效应测量恒星径向速度的办法。光波频率的变化在地球上的人们看来便是星光颜色的变化。如果恒星远离我们而去,则光的谱线就向红光方向移动,称为红移;如果恒星朝向我们运动,光的谱线就向紫光(蓝光)方向移动,称为蓝移。 例如仙女座星系正在朝向银河系奔赴而来,则我们测量来自仙女座星系的光芒时就将发生蓝移现象。一对双星(或者一颗恒星与绕它运转的一颗行星)由于会绕它们的共同质心旋转,故会产生周期性的红移和蓝移。旋涡星系自身旋转时,其正在接近我们的一边会发生蓝移现象,而正在远离我们的一边会发生红移现象。利用这些观察,我们可以测量出遥远天体的运动速度等,并由此推算出其它的一些物理量。
【说明】红移最初是在人们熟悉的可见光波段发现的,随着对电磁波谱各个波段的了解逐步加深,任何电磁辐射的波长增加都可以称为红移。对于波长较短的γ射线、X射线和紫外线等波段,波长变长确实是波谱向红光移动,“红移”的命名并无问题;而对于波长较长的红外线、微波和无线电波等波段,尽管波长增加实际上是远离红光波段,这种现象还是被称为“红移”。“蓝移”也同理。 1912年到1922年间,美国天文学家维斯托·斯里弗观测41个星系的光谱,发现其中的36个星系的光谱发生红移,更进一步的观测还说明这种遥远星系的红移现象在我们的宇宙中似乎普遍存在,继而他推断这些遥远的星系都在不断远离我们的银河系。1929年,美国天文学家哈勃发现距离银河系越远的星系退行越快,于是得到了哈勃定律(在第十篇中已有介绍),成为了“宇宙在膨胀”的观测证据,也成为后来创立大爆炸理论的重要基础。此外,哈勃定律常常被用以直接测量遥远星系的距离,也是我们寻找暗物质的重要工具。
◆ 物理规律的洛伦兹协变性
在本篇的最后,我们回到本篇最开头提出的问题——“相对性原理”来。现在,我们终于可以正式解答这个问题了:怎么才能说明某个物理规律是满足相对性原理的?我们的结论是:只要物理规律的方程能够写成由四维协变量构成的形式,那么它就一定能在洛伦兹变换下保持形式不变,这样就自然满足了相对性原理。
这是为什么呢?首先我们知道,所谓满足“相对性原理”,指的就是在不同的惯性系里物理规律有相同的形式。我们知道,惯性系之间各个物理量的变换是通过洛伦兹变换进行的,因此,只有当这条物理规律里的公式每一项都可以写成同阶的协变量(比方说每一项都是标量、或者说每一项都是矢量、或者说每一项都是二阶张量……),那么对它进行洛伦兹变换(用矩阵\mathbf{\tilde{L}}去作用它),每一项就必然都会按照同样的规律去变化,这样就可以保证方程在变化前后的形式不变。
举个例子,假设某条物理规律在\mathrm{S}系里,可以用如下每一项都是四维矢量的方程表述:
A_{\mu}+B_{\mu \nu}C_{\nu}=D_{\mu}\\
——现在将它换到\mathrm{S}^{'}系中,根据四维协变量满足A_{\mu}^{'}=L_{\mu \nu}A_{\nu}、B_{\mu \nu}^{'}=L_{\mu \alpha}L_{\nu \beta}B_{\alpha \beta}等等性质,我们可以写出:
\begin{eqnarray}A_{\mu}^{'}+B_{\mu \nu}^{'}C_{\nu}^{'}&=&L_{\mu \alpha}A_{\alpha}+L_{\mu \alpha}L_{\nu \beta}B_{\alpha \beta}L_{\nu \eta}C_{\eta}\\&=&L_{\mu \alpha}A_{\alpha}+L_{\mu \alpha}\left( L_{\nu \beta}L_{\nu \eta} \right) B_{\alpha \beta}C_{\eta}\\&=&L_{\mu \alpha}A_{\alpha}+L_{\mu \alpha}\delta _{\beta \eta}B_{\alpha \beta}C_{\eta}\\&=&L_{\mu \alpha}A_{\alpha}+L_{\mu \alpha}B_{\alpha \beta}C_{\beta}\\D_{\mu}^{'}&=&L_{\mu \alpha}D_{\alpha}\end{eqnarray}\\
也就是发现在\mathrm{S}^{'}系里这条物理规律将表述为:
A_{\mu}^{'}+B_{\mu \nu}^{'}C_{\nu}^{'}=D_{\mu}^{'}\\
——具有完全相同的形式,于是便说明了不同惯性系里的物理规律是完全相同的!这种方程在不同惯性系里满足形式不变的性质称作协变性。有时我们也将这种性质说成是洛伦兹协变性(在洛伦兹变换前后能维持形式不变的性质),以与传统的伽利略协变性(在伽利略变换前后能维持方程形式不变的性质)相区分。显然,协变性是一个非常重要的理论概念。
相对性原理假设所有物理规律都能在惯性系下保持不变,这样才能让惯性系之间无法区分,所以也就是说:相对性原理要求所有的物理方程都要满足洛伦兹协变性!基于这一要求,所有的物理方程都应该要能用四维协变量的形式表述出来。
<hr/>本篇开始,我们聚焦狭义相对论的另一条基本假设“相对性原理”——怎样才能保证物理规律在所有惯性系中都不变呢?为了给这条昭示着物理学和谐统一信念的原理以简洁的数学描述,我们将“时间”和“空间”合二为一,构筑出了看似奇异实则严密可靠的四维闵可夫斯基时空,而转换惯性系的洛伦兹变换就这样成为了这个四维时空里坐标架的“旋转”!在四维时空中,我们同样可以定义标量、矢量与张量,曾经熟悉的坐标、速度和波矢等也便有了新的表述。我们最终证明了:物理规律只要能写成协变量的形式,就意味着它能在不同惯性系中保持形式不变。在四维时空里,我们实现了物理规律更高层次、更简洁的统一。
物理学家普遍相信:协变性(相对性原理)是大自然对一切物理规律的共同要求。由此我们必须考察:目前我们已知的那些物理规律,究竟是不是具有协变性呢?具有,则一切安好;不具有,则说明它在考虑相对论效应时会发生矛盾,可能存在缺陷,需要进行适当修正。
检验某个物理规律是否有协变性,就看它能否写成协变量的形式。在下一篇里,我们就要对我们目前已知的两类物理规律——经典力学规律(以牛顿定律为代表)和经典电动力学规律(以麦克斯韦方程组为代表)进行这样的检验。通过使得已知的物理规律自洽地符合相对性原理,我们将进入一个险峻雄奇的高速世界。
欲知后事如何,请听下回分解~ ^_^
<hr/>下一篇:
专栏地址:Stardust · 理论物理初阶
专栏简介与总目录: |